유클리드 기하학과 논증 기하학에 대해 알아보자. 유클리드 기하학은 고대 그리스의 수학자 유클리드가 정립한 기하학으로, 평면과 공간의 성질을 다루는 기초적인 수학 분야이다. 이 기하학은 공리와 정리, 그리고 논증을 통해 수학적 진리를 탐구하는 방법론을 제공한다.
유클리드 기하학의 정의
유클리드 기하학은 기본적으로 평면 기하학과 공간 기하학으로 나뉜다. 평면 기하학은 2차원 공간에서의 도형을 다루고, 공간 기하학은 3차원 공간에서의 도형을 다룬다. 유클리드 기하학의 가장 큰 특징은 공리와 정리를 통해 도형의 성질을 논리적으로 증명하는 것이다. 예를 들어, 두 점을 연결하는 직선은 유일하게 존재하며, 두 직선이 평행할 경우 교차하지 않는다는 원리가 있다. 이러한 원리는 기하학적 사고의 기초가 된다.
유클리드 기하학의 역사
유클리드 기하학은 기원전 300년경에 유클리드가 저술한 "원론"에서 시작되었다. 이 책은 기하학의 기초를 다루며, 13개의 책으로 구성되어 있다. 유클리드는 이 책에서 공리와 정의를 명확히 하고, 이를 바탕으로 다양한 정리를 증명하였다. 유클리드 기하학은 이후 수세기 동안 수학의 기초로 자리 잡았으며, 중세와 르네상스 시대에도 큰 영향을 미쳤다.

논증 기하학의 개념
논증 기하학은 유클리드 기하학의 한 형태로, 수치적인 계산보다는 도형의 성질과 관계를 중시한다. 이 기하학은 도형의 성질을 논리적으로 증명하는 데 중점을 두며, 수학적 사고를 발전시키는 데 중요한 역할을 한다. 논증 기하학은 기하학적 원리를 이해하고, 이를 바탕으로 문제를 해결하는 능력을 기르는 데 도움을 준다.
유클리드 기하학과 논증 기하학의 차이점
유클리드 기하학과 논증 기하학의 가장 큰 차이는 접근 방식에 있다. 유클리드 기하학은 공리와 정리를 통해 기하학적 사실을 증명하는 반면, 논증 기하학은 도형의 성질을 바탕으로 논리적 추론을 통해 문제를 해결한다. 예를 들어, 유클리드 기하학에서는 평행선의 성질을 공리로 두고 이를 바탕으로 다양한 정리를 증명하지만, 논증 기하학에서는 이러한 성질을 직접적으로 관찰하고 논리적으로 설명하는 데 중점을 둔다.
유클리드 기하학의 주요 원리
유클리드 기하학의 주요 원리는 다음과 같다:
- 공리 : 기하학의 기본적인 진리로, 증명이 필요 없는 사실이다.
- 정리 : 공리와 정의를 바탕으로 증명된 사실이다.
- 논증 : 정리를 증명하기 위한 논리적 과정이다.
이러한 원리는 기하학적 사고를 발전시키고, 수학적 문제를 해결하는 데 필수적이다.
유클리드 기하학의 응용
유클리드 기하학은 건축, 공학, 컴퓨터 그래픽스 등 다양한 분야에서 응용된다. 예를 들어, 건축에서는 구조물의 안정성을 확보하기 위해 기하학적 원리를 활용하며, 컴퓨터 그래픽스에서는 3D 모델링과 애니메이션 제작에 유클리드 기하학의 원리를 적용한다.
비유클리드 기하학과의 비교
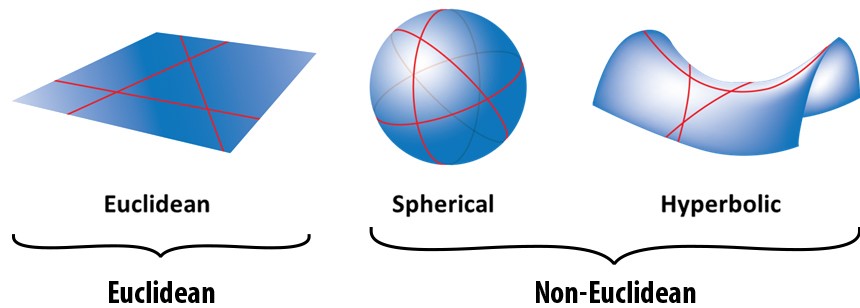
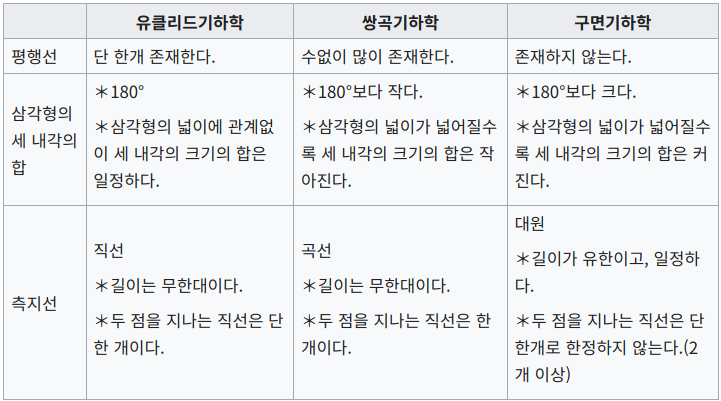
비유클리드 기하학은 유클리드 기하학의 공리 중 하나인 평행선 공리를 부정하는 기하학이다. 비유클리드 기하학에는 구면 기하학과 쌍곡선 기하학이 포함된다. 구면 기하학에서는 평행선이 존재하지 않으며, 쌍곡선 기하학에서는 무한히 많은 평행선이 존재한다. 이러한 비유클리드 기하학은 현대 물리학과 우주론에서도 중요한 역할을 한다.
유클리드 기하학의 현대적 의미
오늘날 유클리드 기하학은 수학 교육의 기초로 여전히 중요한 위치를 차지하고 있다. 학생들은 유클리드 기하학을 통해 논리적 사고와 문제 해결 능력을 기를 수 있으며, 이는 다양한 분야에서의 학습과 연구에 큰 도움이 된다. 또한, 유클리드 기하학의 원리는 현대 수학의 많은 분야에 여전히 적용되고 있다.
유클리드 기하학과 논증 기하학은 수학의 기초를 이루는 중요한 개념이다. 이 두 가지 기하학을 이해함으로써 우리는 수학적 사고를 발전시키고, 다양한 문제를 해결하는 데 필요한 능력을 기를 수 있다.
유클리드 기하학의 원리와 논증 기하학의 접근 방식을 통해 우리는 수학의 아름다움과 논리적 사고의 중요성을 깨닫게 된다. 이러한 기하학적 원리는 단순한 수학적 사실을 넘어, 우리의 사고 방식을 형성하는 데 큰 영향을 미친다.

태그
#유클리드기하학 #논증기하학 #수학 #기하학 #비유클리드기하학 #수학적사고 #기하학의역사 #논리적사고 #수학교육 #기하학적원리
이런 자료를 참고 했어요.
[1] 나무위키 - 논증 기하학 (https://namu.wiki/w/%EB%85%BC%EC%A6%9D%20%EA%B8%B0%ED%95%98%ED%95%99)
[2] 네이버 블로그 - 기하학의 역사와 유클리드 기하학(feat. 유클리드 평행공준) (https://m.blog.naver.com/ryumochyee-logarithm/221898392892)
[3] 나무위키 - 논증 기하학 (r35 판) (https://namu.wiki/w/%EB%85%BC%EC%A6%9D%20%EA%B8%B0%ED%95%98%ED%95%99?uuid=3d26401f-4514-4d7e-a5af-186eaecd3da8)
[4] Korea Science - 신라대학교 수학교육과 김태완 (https://koreascience.or.kr/article/JAKO200412910520265.pdf)
'수학' 카테고리의 다른 글
| 물가 수준의 변화를 보여주는 함수, 물가지수 (0) | 2025.01.26 |
|---|---|
| 복불복 게임 먼저 뽑는게 유리한가? (0) | 2025.01.26 |
| 머피의 법칙이란? (0) | 2025.01.26 |
| 몬티홀 문제의 답은? (0) | 2025.01.25 |
| 테일러 급수 (0) | 2025.01.25 |
