몬티홀 문제는 많은 사람들에게 혼란을 주는 흥미로운 확률 문제입니다. 이 문제는 세 개의 문 중 하나를 선택하고, 그 뒤에 숨겨진 상품을 찾는 게임으로, 많은 사람들이 직관적으로 잘못된 결정을 내리곤 합니다. 이번 포스팅에서는 몬티홀 문제의 기본 개념부터 시작해, 확률, 전략, 실제 예시, 수학적 설명, 응용까지 자세히 알아보겠습니다. 🚪🚗
몬티홀 문제란?
몬티홀 문제는 미국의 유명한 게임쇼 "Let's Make a Deal"에서 유래된 문제입니다. 이 게임에서는 참가자가 세 개의 문 중 하나를 선택하고, 그 뒤에 숨겨진 상품을 찾는 방식으로 진행됩니다. 한 문 뒤에는 자동차와 같은 큰 상품이 있고, 나머지 두 문 뒤에는 염소가 있습니다. 참가자가 문을 선택한 후, 진행자는 선택하지 않은 문 중 하나를 열어 염소를 보여줍니다. 그 후, 참가자는 처음 선택한 문을 유지할지, 아니면 다른 문으로 변경할지를 결정해야 합니다. 이 과정에서 어떤 선택이 더 유리한지에 대한 논의가 이루어집니다.
문제의 기본 구조
몬티홀 문제의 기본 구조는 다음과 같습니다. 참가자는 세 개의 문 중 하나를 선택합니다. 그 후 진행자는 선택하지 않은 문 중 하나를 열어 염소를 보여줍니다. 이때 참가자는 처음 선택한 문을 유지할지, 아니면 다른 문으로 변경할지를 결정해야 합니다. 이 과정에서 중요한 점은 진행자가 항상 염소가 있는 문을 열기 때문에, 선택의 기회가 바뀐다는 것입니다.
확률의 이해
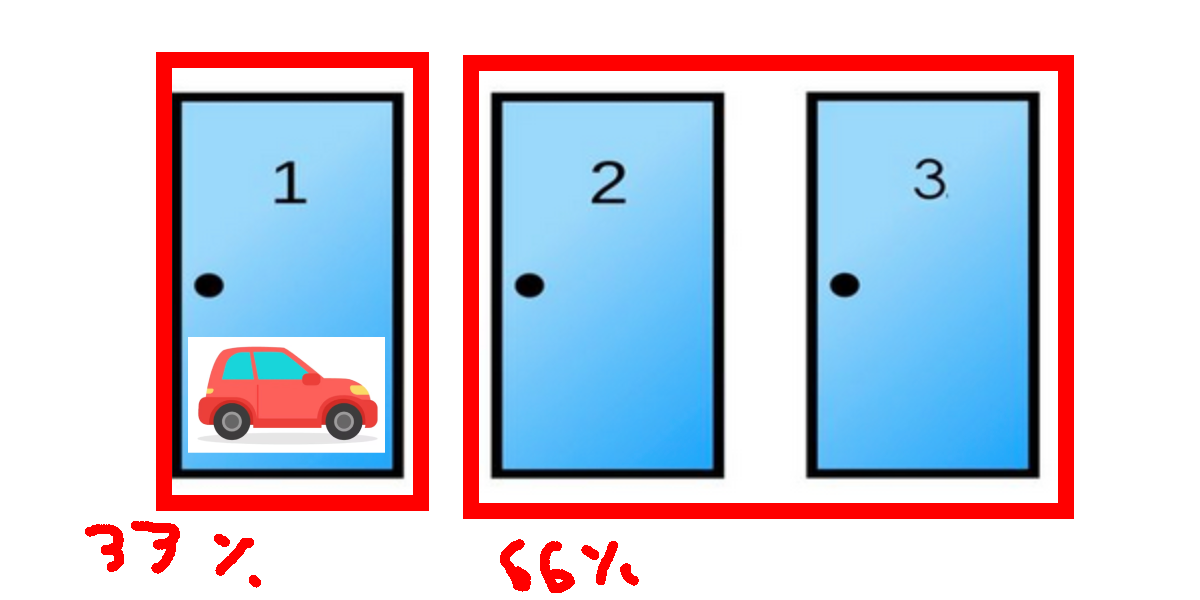
몬티홀 문제에서의 확률은 매우 흥미롭습니다. 처음 문을 선택할 때, 자동차가 그 문 뒤에 있을 확률은 1/3입니다. 반면, 나머지 두 문 중 하나에 자동차가 있을 확률은 2/3입니다. 진행자가 염소가 있는 문을 열고 나면, 남은 문 중 하나는 여전히 1/3의 확률을 가지지만, 다른 문은 2/3의 확률로 자동차가 숨겨져 있습니다. 따라서, 문을 변경하는 것이 더 유리하다는 결론에 도달하게 됩니다.

전략: 선택 후 변경하기
많은 사람들이 처음 선택한 문을 고수하는 경향이 있지만, 몬티홀 문제의 전략은 문을 변경하는 것입니다. 문을 변경하면 승리할 확률이 2/3로 증가합니다. 이는 진행자가 염소가 있는 문을 열어주기 때문에 가능한 전략입니다. 따라서, 처음 선택한 문을 고수하는 것보다 변경하는 것이 더 나은 선택이 됩니다.
몬티홀 문제의 실제 예시
실제 예시를 통해 몬티홀 문제를 더 잘 이해할 수 있습니다. 예를 들어, 참가자가 1번 문을 선택했다고 가정해봅시다. 진행자는 3번 문을 열어 염소를 보여줍니다. 이제 참가자는 1번 문을 유지할지, 2번 문으로 변경할지를 결정해야 합니다. 이 경우, 1번 문 뒤에 자동차가 있을 확률은 여전히 1/3이지만, 2번 문 뒤에 자동차가 있을 확률은 2/3로 증가합니다. 따라서, 2번 문으로 변경하는 것이 더 유리합니다.

몬티홀 문제의 수학적 설명
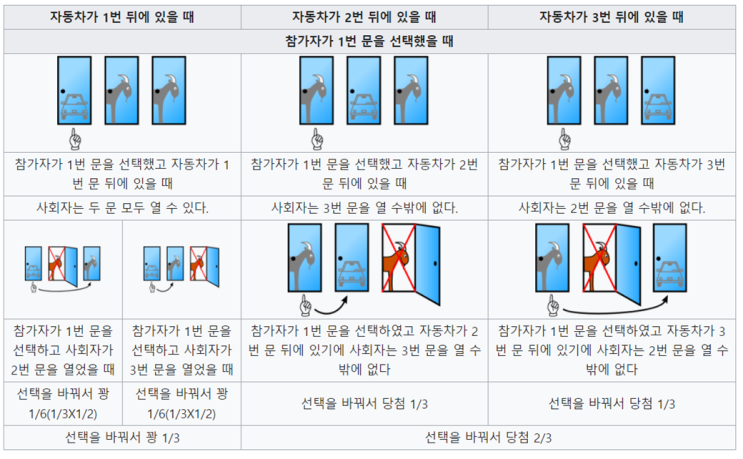
몬티홀 문제를 수학적으로 설명하면, 다음과 같은 방식으로 접근할 수 있습니다. 참가자가 처음 선택한 문이 자동차가 있는 경우(1/3 확률)와 염소가 있는 경우(2/3 확률)를 나누어 생각할 수 있습니다. 만약 참가자가 처음 선택한 문이 자동차라면, 문을 변경하면 패배하게 됩니다. 그러나 처음 선택한 문이 염소라면, 문을 변경하면 승리하게 됩니다. 따라서, 문을 변경하는 전략이 더 유리하다는 것을 알 수 있습니다.
몬티홀 문제의 응용
몬티홀 문제는 단순한 게임의 예시일 뿐만 아니라, 실제 생활에서도 응용될 수 있습니다. 예를 들어, 의사 결정 과정에서의 선택, 투자 전략, 마케팅 전략 등 다양한 분야에서 이 문제의 원리를 적용할 수 있습니다. 확률과 선택의 중요성을 이해하는 데 큰 도움이 됩니다.
자주 묻는 질문
- 왜 문을 변경하는 것이 더 유리한가요?
- 문을 변경하면 승리할 확률이 2/3로 증가하기 때문입니다.
- 이 문제는 실제로 어떻게 적용될 수 있나요?
- 의사 결정, 투자, 마케팅 등 다양한 분야에서 확률을 고려한 선택이 중요합니다.
- 몬티홀 문제는 왜 많은 사람들에게 혼란을 주나요?
- 직관적으로는 처음 선택한 문을 고수하는 것이 더 안전하다고 생각하기 때문입니다.
마무리
몬티홀 문제는 단순한 게임이지만, 그 이면에는 확률과 전략에 대한 깊은 통찰이 숨겨져 있습니다. 이 문제를 통해 우리는 선택의 중요성과 확률의 개념을 더욱 잘 이해할 수 있습니다. 다음에 의사 결정을 할 때, 몬티홀 문제를 떠올리며 더 나은 선택을 하길 바랍니다! 🚀
태그: #몬티홀문제 #확률 #게임이론 #의사결정 #전략
이런 자료를 참고 했어요.
[1] 나무위키 - 몬티 홀 문제 (https://namu.wiki/w/%EB%AA%AC%ED%8B%B0%20%ED%99%80%20%EB%AC%B8%EC%A0%9C)
[2] Wikipedia - 몬티 홀 문제 - 위키백과, 우리 모두의 백과사전 (https://ko.wikipedia.org/wiki/%EB%AA%AC%ED%8B%B0_%ED%99%80_%EB%AC%B8%EC%A0%9C)
[3] velog - 몬티홀 문제 쉽게 설명 (https://velog.io/@adguy/%EB%AA%AC%ED%8B%B0%ED%99%80-%EB%AC%B8%EC%A0%9C-%EC%89%BD%EA%B2%8C-%EC%84%A4%EB%AA%85)
[4] NAVER - 몬티홀 문제(몬티홀 딜레마) 가장 쉽게 이해하기 (https://blog.naver.com/jjaprince/220278302374)
'수학' 카테고리의 다른 글
| 유클리드 기하학과 논증 기하학 (0) | 2025.01.26 |
|---|---|
| 머피의 법칙이란? (0) | 2025.01.26 |
| 테일러 급수 (0) | 2025.01.25 |
| 세상에서 가장 아름다운 수식, 오일러 공식 (0) | 2025.01.25 |
| 곱셈 3초컷 계산법 (특이한 케이스) (0) | 2024.04.07 |
