반응형
- 99 곱하기 한 자리수의 규칙성
99x1=99
99x2=198
99x3=297
99x4=396
99x5=495
99x6=594
99x7=693
99x8=792
99x9=891
규칙을 찾으셨나요?
99x3을 예시로 들면

9를 먼저 가운데에 쓰고 9x3=27의 값을 9의 양옆에 차례대로 써주시면 됩니다.
(참고로 99x1은 9x1=09로 놓고 써주세요 그러면 099이므로 99입니다.)
- 99곱하기 두자리수의 규칙성 (단, 99x10이나 99x70같은 일의 자리숫자에 0이 들어가는 숫자는 0을 뺀 상태로 '99곱하기 한자리수 규칙' 대로 계산하고 0을 뒤에 붙여야됨.)
99x11=1089
99x12=1188
99x13=1287
99x14=1386
99x15=1485
.
.
.
99x36=3564
99x37=3663
규칙성이 보이시나요?
99x89를 예시로 들면

이 방식을 사용하면 9가 한없이 많아도 9와 자리수가 같은 수를 곱한다면 빠른 계산을 할 수 있다.
예를들어 99999x47839의 값을 구하고 싶으면 위에서 사용한 방식을 사용해서 이런식으로 계산할 수 있다.
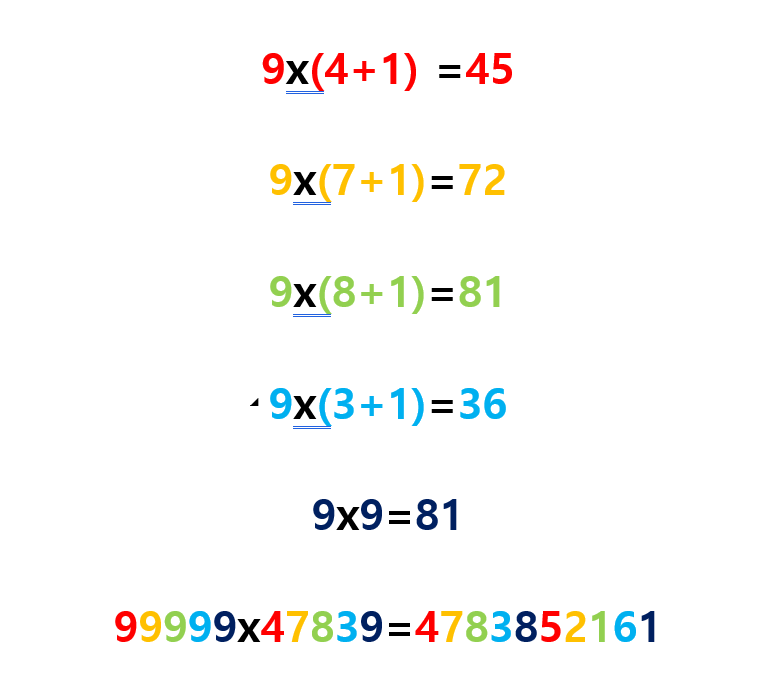
마지막에 곱하는 수만 그대로 곱하고 나머지 수는 1씩 더해 곱한 후 자리수에 맞게 쓰면 답이된다.

실제 계산결과와 일치하는 것을 볼 수 있다.
이 큰 숫자를 다섯번의 간단한 계산만을 통해 구할 수 있다는 것이 놀랍지 않은가........
지금까지 9의 신기한 성질(?) 에 대해서 알아보았다. 이러한 방식을 사용하면 여러번 곱해야되는 큰 숫자의 계산을 계산기보다 빠르게 계산 할 수 있게된다. (아마도....? 숫자 치는시간이 더 오래걸림)
반응형
'수학' 카테고리의 다른 글
| 머피의 법칙이란? (0) | 2025.01.26 |
|---|---|
| 몬티홀 문제의 답은? (0) | 2025.01.25 |
| 테일러 급수 (0) | 2025.01.25 |
| 세상에서 가장 아름다운 수식, 오일러 공식 (0) | 2025.01.25 |
| 정 무한각형=원 증명 과정 (2) | 2024.04.07 |
